基于EMD分解的谐波检测方法

摘  要:  本文把经验模式分解（EMD）应用于有源滤波器的谐波检测中。对谐波电流进行EMD分解，得到一系列固有模态函数（IMF），由于EMD 分解的完备性，不同的IMF 代表了不同的频率分量，即得到基波和各次谐波IMF 分量，从而完成谐波的检测。仿真结果表明，基于EMD 的谐波检测方法，不仅能有效地将电力系统谐波自适应地分离出来，而且对于有源滤波器的谐波检测具有较高的实时性。

关键词:  EMD  谐波检测  有源电力滤波器

1. 引言

随着电力电子设备的广泛应用，电网的谐波污染问题越来越严重。有源电力滤波器（APF）由于有极快的跟踪速度、极好的补偿性能，得到了快速的发展和应用。采用有源电力滤波器滤除谐波已经成为一个重要的研究方向^[1]。而准确地检测出谐波是决定补偿效果的重要环节。目前，国内外学者已经提出了大量的谐波电流检测方法，按照检测分析的数学方法的不同，可以把这些方法分为频域法和时域法两大类。频域法主要包括两种方法：滤波器分离方法、FFT 检测方法和小波变换的分析法^[2]；时域法主要有：瞬时无功理论^[3]、自适应检测法和神经网络法等。

但是这些谐波检测方法都有其优缺点，FFT 检测法需要进行两次变换，计算量大，计算时间长，故检测时间较长，检测结果的实时性较差；基于瞬时无功功率理论检测法的时间延迟取决于低通滤波器的性能，同时理想低通滤波器的物理实现困难。所检测出基波电流有大半个周期的延迟；小波函数能量不集中，容易造成频谱混叠。同时小波变换本质是一种基于基函数展开的理论，信号分析结果很大程度上依赖基函数的选择，而对一个具体问题而言，最优基的选择没有确定的规则可循，所以小波基函数的选择是个难题；自适应检测法虽然能够自动跟踪信号频率，但由于其响应速度与滤波效果是矛盾的，通常为了保证滤波效果，会导致谐波分离的实时性变差。

希尔伯特-黄变换^[4-5]（Hilbert-Huang Transform，HHT）是1998年Huang等人提出的一种新的信号分析理论。该理论提出了固有模态函数（Intrinsic Mode Function，IMF）并引入经验模态分解方法（Empirical Mode Decomposition，EMD），特别适用于分析现实生活中存在的大量频率随时间变化的非线性、非平稳信号。对于一个非平稳的数据信号来讲，Hilbert变换得到的结果很大程度上失去了原有的物理意义，而经EMD分解得到的结果能够反映真实的物理过程，由此得到的Hilbert谱能够准确地反映出该物理过程中能量在空间（或时间）各种尺度上的分布规律，因此EMD方法为非平稳数据进行Hilbert变换奠定了基础。目前该方法已被应用于机械故障诊断、海洋、医学信号处理、电能质量检测等领域^[6]。

2. EMD基本原理

HHT变换的核心是EMD分解，EMD 的出发点就是把局部信号分解为若干个IMF，IMF需满足2 个条件：①极值点数和零点数相差不大于1；② IMF 的均值趋于零。对于任意信号x(t) ，Hilbert-Huang 变换的算法可以描述如下：设信号变量x(t)的初始值为 令i=1 对其进行如下操作：①求得x(t)的所有极值点；②在极值点间用三次样条函数进行插值，得到上、下包络线和；③计算均值线；④提取细节；⑤判断d(t)是否满足IMF 的2 个条件如果满足则令=d(t)转入步骤⑥，如果不满足，则令x(t)=d(t) 重复执行步骤①~⑤；⑥；⑦判断是否是单调函数，如果是，则循环结束否，则令转到步骤①。

当循环结束时，得到了n 个满足条件的IMF 分量，这时令,称为残余分量这样可得到EMD 的分解结果为：

   (1)

因此IMF 分量分别包含了信号从高到低不同频率成分，而则表示信号的余量。

有源滤波器的谐波检测环节要求输出电网谐波，其原理就是将电网中的基波分量和谐波分量分开，达到检测谐波的目的。根据式（1）可知，当把看作测量误差时，有

   (2)

式中表示各次谐波的IMF 分量之和；为基波的IMF 分量；为余量。则由式（2）可知，基波和谐波完成分离，即完成了谐波检测。

EMD分解在每一时刻首先分解出尺度最小的IMF，然后分解出尺度较大的IMF，然后再分解出尺度更大的IMF。阶数越低，其含有的高频成分越多。不同的IMF 代表了不同的频率分量，因此，将这种方法用到谐波检测中，能很好地得到基波和各次谐波IMF 分量，从而完成谐波的检测。

3.仿真验证

假定电网信号：

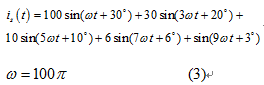
对于这个电网信号，考虑到实际的电网信号，加入高斯白噪声，进行分析。

由于EMD是根据信号局部特征从小尺度到大尺度逐次将信号分为不同时间尺度的IMF分量，所以，图1-1中的imf1可以看成高频噪声。图1-2为基波IMF分量及谐波，图1-3为基波IMF分量幅频谱，可以看出，HHT方法准确检测出了基波分量，即检测出电网谐波。

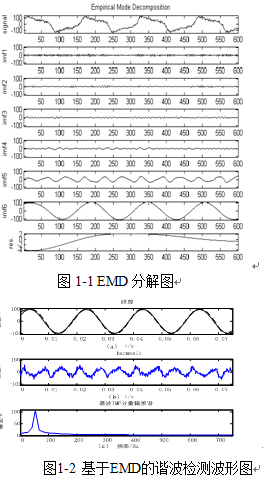
为了突出基于HHT方法的优越性，对同样信号分别进行小波法检测和基于瞬时无功功率理论方法的谐波检测。图1-3为三种检测方法的跟踪性能对比。

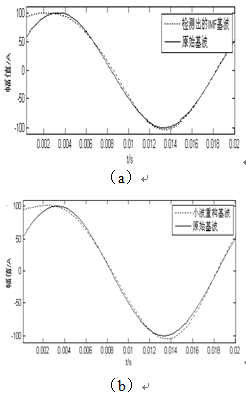
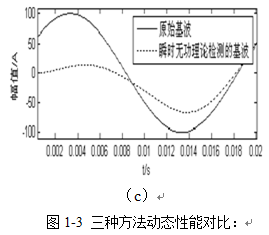
（a）HHT方法；（b）小波检测法；（c）瞬时无功理论方法

表1列出了三种方法检测出的基波的频率、幅值及动态响应时间，可以看出，基于瞬时无功功率理论检测法的精度是最好的，但其动态响应时间则接近一个周期，这是由低通滤波器的延迟造成的；在相同的检测精度下，基于HHT检测法响应时间大约为3/20周期，小波检测在2/5周期才完全跟踪上原始基波。可以看出，HHT检测结果动态跟踪性能比小波和瞬时无功功率理论方法都要好。

表1 三种方法对比

4.总结

仿真结果表明，基于HHT的检测法可以有效、快速准确检测出电网谐波分量。通过比较瞬时无功功率检测法、小波检测法及HHT检测法处理同一信号的仿真结果，HHT方法不存在小波变换基函数的选择问题，可以自适应分离谐波，而且相对于瞬时无功功率检测法具有更好的实时性。

参考文献

[1]                王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].第二版.北京:机械工业出版社，1998

[2]                杨颀.基于瞬时无功功率和小波变换的谐波测量湖南大学硕士学文论文2003

[3]                付振宇,刘觉民,张彦林.瞬时检测谐波及无功电流的单相有源滤波器研究[J]. 电气传动, 2006(3)：29-31

[4]                Huang N E，Shen Zheng，et al. The empirical code decomposition and the Hilbert spectrum for nonlinear and nonlinear and non-stationary timeseries analysis[R]. Royal Society, 1998(454): 915-995.

[5]                Rilling G, Flandrin P, Goncalves P. On empirical mode decomposition and its algorithms[C]. IEEE-EURASIP    Workshop on Nonlinear Signal and Image Processing, Grado(I), 2003.

[6]                李天云，赵妍，李楠等.基于HHT的电能质量检测新方法[J].中国电机工程学报, 2005(9):52-56